Neural Networks has the advantage of fitting responses of any shape or configuration, that usual analytic form can not or very hard to describe. See this 2-D spiral pattern, usual modeling technique will have a hard time to detect and fit the spirals, i.e. there no linear form that can be used to identify these spirals:
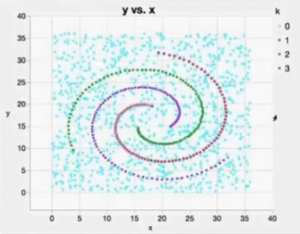
By fitting a Neural Network model we able to associate points on the plot to each of the three spirals.
Neural Networks models also possess some sort of intuition or connection to everyday people’s understanding of cause and consequences. Factors and inner mechanism may be interrelated and opaque, but the inputs and results are mostly known and limited in numbers, see this example about understanding and therefore to predict future Boston area housing values:
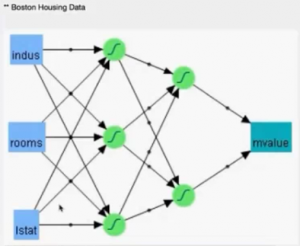
The building of Neural Networks model is mostly composed by theses steps:
- Activation functions and hidden layer structure: number of layers and number of nodes under each activation functions: TanH, Linear, and Gaussian, where
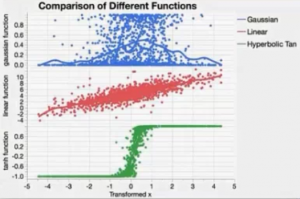
- TanH: The hyperbolic tangent function is a sigmoid function (S-shaped, as logistic curves). TanH transforms values to be tween -1 and 1, and is the centered and scaled version of the logistic function
- Linear: Most often used in conjunction with one of the non-linear activation functions. For example, place the linear activation function in the second layer, and the non-linear activation functions in the first layer. This would be useful if you want to first reduce the dimentionality of the X variables, and then have nonlinear model for the Y variables. For a continuous Y variable, if only Linear activation functions are used, the model for the y variable reduces to a linear combination of the X variables. For a nominal or ordinal Y variable, the model reduces to a logistic regression.
- Gaussian: This function is used for responses display radial function behavior, or when the response surface is known as Gaussian (normal) in shape.Below is a comparison the fitting patterns for different data distributions from different activation functions:

- Boosting: four important points to keep in mind.
- Boosting is building a large additive neural network model by fitting a sequence of smaller models
- and each of the smaller models fit on the scaled residuals of the previous model. The models are combined to form the larger final model
- Boosting is often faster than fitting a single large model. However, the base model should be a 1 to 2 node single-layer model, or else the benefit of faster fitting can be lost if a large number of model is specified
- The learning rate must be 0<1<=1. Learning rates close to 1 result in faster convergence on a final model, but also have a higher tendency to over-fit data. To specify a bigger learning rate will result in taking bigger learning steps in each iteration of boosting, smaller learning rate vice versa. The trade off is smaller learning rate will take longer time and may result in over-fitting, versus larger steps with faster completion but with likelihood of missing certain useful information. The usual learning rate to use is 0.01 (or 10%). Therefore the fitted model should be validated the same time it is boosted, i.e., stop boosting if the R-square from the validation model stopped from improving.
- Fitting options: whether to transform the covariates, the penalty methods to choose, and the number of “tours”. Covariates may be transformed to normal; penalty may be taken to reflect the emphasis put on the covariates, choices are square, absolute deviation with weight decaying and no penalty; “tours” are the random start model fittings that ended with different model estimates, that are averaged to constructed the “ensemble model estimate
- Search progression
Reviewing Concepts
Both input and output (response) variables could be either continuous or categorical.
Validation can prevent over-fitting, as over-fitted model tend not do well when using new data.
NN estimation starts with a random guess of the estimate, then the whole algorithm with improve until the best estimate at the end of the iterations. However the end estimate may be different depending on where the initial random guessing is. So the “ensemble method” takes a number of random starts, and the final estimate takes the average of the estimates.
The “confusion matrix” by number or rate may be convincing checking points; also the R-square on both the training and validation data ideally should be high and close to each other
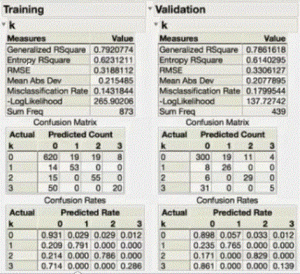
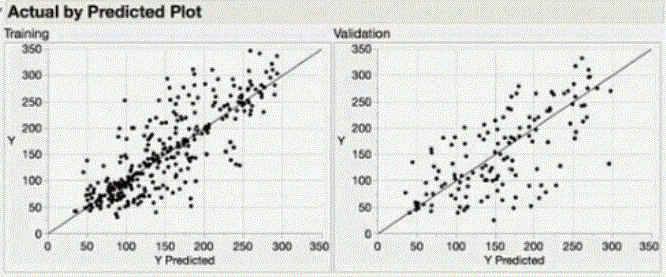
Actual vs. Predicted plots both on the training and validation sets for continuous responses are a good visual aid (straight line) to exam model fitting
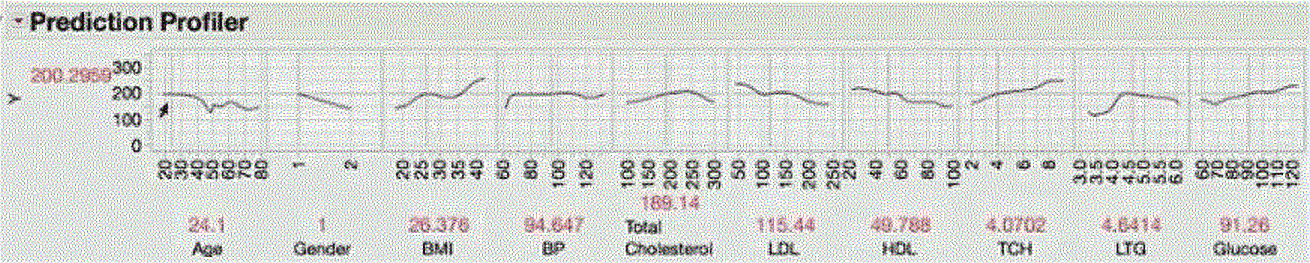
A “visual profiler” are useful to visualize the impact of each covariate on the response (probability of each category for category responses), under the fitted model, and how the changing of inputs one-at-a-time may impact the response, as well location of the inputs on at each level of the response
Nodes on the hidden layers are constructed in the way very similarly to principal components (PCs), i.e. reducing the high dimension of input nodes to one by expressing one linear combination of the inputs. NN builds the PCs along the way, but may not be linear
Statistical tools fitting the NN models should better be able to provide the final fitted formula so the model can be transported across platforms, say to Excel, SAS, Python, Java etc.
Research Terms
Learning Rate
(Neural networks overview and case studies)